文章目录
  1. 1 概述
    1. 1.1 传统哈希(硬哈希)
    2. 1.2 一致性哈希(Consistent Hashing)
    3. 1.3 哈希指标
    4. 1.4 资料链接
  2. 2 算法原理
    1. 2.1 映射方案
      1. 2.1.1 公用哈希函数和哈希环
      2. 2.1.2 节点(Node)映射至哈希环
      3. 2.1.3 对象(Object)映射于哈希环
      4. 2.1.4 对象(Object)映射至节点(Node)
    2. 2.2 删除节点
    3. 2.3 增加节点
    4. 2.4 虚拟节点
  3. 3 算法实现
    1. 3.1 源码
    2. 3.2 复制倍数为 1 时的均衡性
    3. 3.2 复制倍数为 32 时的均衡性
    4. 3.2 复制倍数为 1M 时的均衡性
  4. 4 应用

分布式系统中对象与节点的映射关系，传统方案是使用对象的哈希值，对节点个数取模，再映射到相应编号的节点，这种方案在节点个数变动时，绝大多数对象的映射关系会失效而需要迁移；而一致性哈希算法中，当节点个数变动时，映射关系失效的对象非常少，迁移成本也非常小。本文总结了一致性哈希的算法原理和Java实现，并列举了其应用。

作者：王克锋
出处：https://kefeng.wang/2018/08/10/consistent-hashing/
版权：自由转载-非商用-非衍生-保持署名，转载请标明作者和出处。

1 概述

1.1 传统哈希(硬哈希)

分布式系统中，假设有 n 个节点，传统方案使用 mod(key, n) 映射数据和节点。
当扩容或缩容时(哪怕只是增减1个节点)，映射关系变为 mod(key, n+1) / mod(key, n-1)，绝大多数数据的映射关系都会失效。

1.2 一致性哈希(Consistent Hashing)

1997年，麻省理工学院(MIT)的 David Karger 等6个人发布学术论文《Consistent hashing and random trees: distributed caching protocols for relieving hot spots on the World Wide Web（一致性哈希和随机树：用于缓解万维网上热点的分布式缓存协议）》，对于 K 个关键字和 n 个槽位(分布式系统中的节点)的哈希表，增减槽位后，平均只需对 K/n 个关键字重新映射。

1.3 哈希指标

评估一个哈希算法的优劣，有如下指标，而一致性哈希全部满足：

  • 均衡性(Balance)：将关键字的哈希地址均匀地分布在地址空间中，使地址空间得到充分利用，这是设计哈希的一个基本特性。
  • 单调性(Monotonicity): 单调性是指当地址空间增大时，通过哈希函数所得到的关键字的哈希地址也能映射的新的地址空间，而不是仅限于原先的地址空间。或等地址空间减少时，也是只能映射到有效的地址空间中。简单的哈希函数往往不能满足此性质。
  • 分散性(Spread): 哈希经常用在分布式环境中，终端用户通过哈希函数将自己的内容存到不同的缓冲区。此时，终端有可能看不到所有的缓冲，而是只能看到其中的一部分。当终端希望通过哈希过程将内容映射到缓冲上时，由于不同终端所见的缓冲范围有可能不同，从而导致哈希的结果不一致，最终的结果是相同的内容被不同的终端映射到不同的缓冲区中。这种情况显然是应该避免的，因为它导致相同内容被存储到不同缓冲中去，降低了系统存储的效率。分散性的定义就是上述情况发生的严重程度。好的哈希算法应能够尽量避免不一致的情况发生，也就是尽量降低分散性。
  • 负载(Load): 负载问题实际上是从另一个角度看待分散性问题。既然不同的终端可能将相同的内容映射到不同的缓冲区中，那么对于一个特定的缓冲区而言，也可能被不同的用户映射为不同的内容。与分散性一样，这种情况也是应当避免的，因此好的哈希算法应能够尽量降低缓冲的负荷。

1.4 资料链接

原始论文《Consistent Hashing and Random Trees》链接如下：

相关论文《Web Caching with Consistent Hashing》链接如下：

更多资料：
WikiPedia - Consistent hashing
codeproject - Consistent hashing

2 算法原理

2.1 映射方案

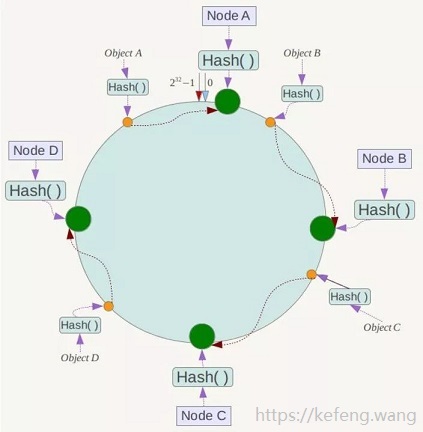
2.1.1 公用哈希函数和哈希环

设计哈希函数 Hash(key)，要求取值范围为 [0, 2^32)
各哈希值在上图 Hash 环上的分布：时钟12点位置为0，按顺时针方向递增，临近12点的左侧位置为2^32-1。

2.1.2 节点(Node)映射至哈希环

如图哈希环上的绿球所示，四个节点 Node A/B/C/D，
其 IP 地址或机器名，经过同一个 Hash() 计算的结果，映射到哈希环上。

2.1.3 对象(Object)映射于哈希环

如图哈希环上的黄球所示，四个对象 Object A/B/C/D，
其键值，经过同一个 Hash() 计算的结果，映射到哈希环上。

2.1.4 对象(Object)映射至节点(Node)

在对象和节点都映射至同一个哈希环之后，要确定某个对象映射至哪个节点，
只需从该对象开始，沿着哈希环顺时针方向查找，找到的第一个节点，即是。
可见，Object A/B/C/D 分别映射至 Node A/B/C/D。

2.2 删除节点

现实场景：服务器缩容时删除节点，或者有节点宕机。如下图，要删除节点 Node C：
只会影响欲删除节点(Node C)与上一个(顺时针为前进方向)节点(Node B)与之间的对象，也就是 Object C，
这些对象的映射关系，按照 2.1.4 的规则，调整映射至欲删除节点的下一个节点 Node D。
其他对象的映射关系，都无需调整。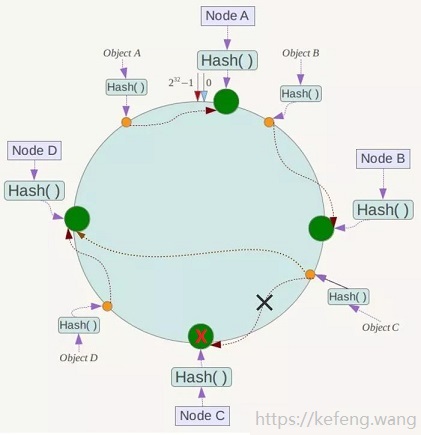

2.3 增加节点

现实场景：服务器扩容时增加节点。比如要在 Node B/C 之间增加节点 Node X：
只会影响欲新增节点(Node X)与上一个(顺时针为前进方向)节点(Node B)与之间的对象，也就是 Object C，
这些对象的映射关系，按照 2.1.4 的规则，调整映射至新增的节点 Node X。
其他对象的映射关系，都无需调整。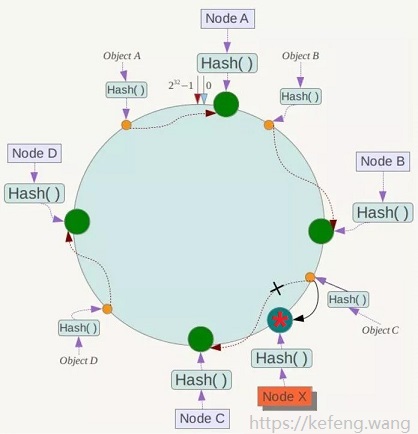

2.4 虚拟节点

对于前面的方案，节点数越少，越容易出现节点在哈希环上的分布不均匀，导致各节点映射的对象数量严重不均衡(数据倾斜)；相反，节点数越多越密集，数据在哈希环上的分布就越均匀。
但实际部署的物理节点有限，我们可以用有限的物理节点，虚拟出足够多的虚拟节点(Virtual Node)，最终达到数据在哈希环上均匀分布的效果：
如下图，实际只部署了2个节点 Node A/B，
每个节点都复制成3倍，结果看上去是部署了6个节点。
可以想象，当复制倍数为 2^32 时，就达到绝对的均匀，通常可取复制倍数为32或更高。
虚拟节点哈希值的计算方法调整为：对“节点的IP(或机器名)+虚拟节点的序号(1~N)”作哈希。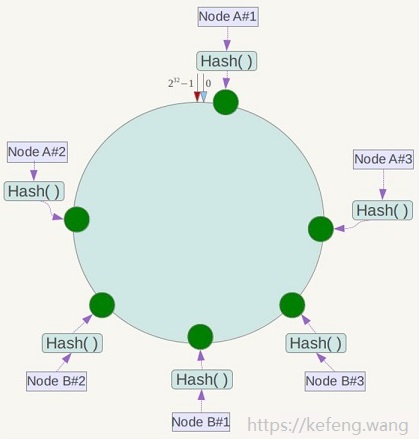

3 算法实现

一致性哈希算法有多种具体的实现，包括 Chord 算法，KAD 算法等，都比较复杂。
这里给出一个简易实现及其演示，可以看到一致性哈希的均衡性和单调性的优势。
单调性在本例中没有统计数据，但根据前面原理可知，增删节点后只有很少量的数据需要调整映射关系。

3.1 源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
/**
 * @author: https://kefeng.wang
 * @date: 2018-08-10 11:08
 **/
public class ConsistentHashing {
    // 物理节点
    private Set<String> physicalNodes = new TreeSet<String>() {
        {
            add("192.168.1.101");
            add("192.168.1.102");
            add("192.168.1.103");
            add("192.168.1.104");
        }
    };

    //虚拟节点
    private final int VIRTUAL_COPIES = 1048576; // 物理节点至虚拟节点的复制倍数
    private TreeMap<Long, String> virtualNodes = new TreeMap<>(); // 哈希值 => 物理节点

    // 32位的 Fowler-Noll-Vo 哈希算法
    // https://en.wikipedia.org/wiki/Fowler–Noll–Vo_hash_function
    private static Long FNVHash(String key) {
        final int p = 16777619;
        Long hash = 2166136261L;
        for (int idx = 0, num = key.length(); idx < num; ++idx) {
            hash = (hash ^ key.charAt(idx)) * p;
        }
        hash += hash << 13;
        hash ^= hash >> 7;
        hash += hash << 3;
        hash ^= hash >> 17;
        hash += hash << 5;

        if (hash < 0) {
            hash = Math.abs(hash);
        }
        return hash;
    }

    // 根据物理节点，构建虚拟节点映射表
    public ConsistentHashing() {
        for (String nodeIp : physicalNodes) {
            addPhysicalNode(nodeIp);
        }
    }

    // 添加物理节点
    public void addPhysicalNode(String nodeIp) {
        for (int idx = 0; idx < VIRTUAL_COPIES; ++idx) {
            long hash = FNVHash(nodeIp + "#" + idx);
            virtualNodes.put(hash, nodeIp);
        }
    }

    // 删除物理节点
    public void removePhysicalNode(String nodeIp) {
        for (int idx = 0; idx < VIRTUAL_COPIES; ++idx) {
            long hash = FNVHash(nodeIp + "#" + idx);
            virtualNodes.remove(hash);
        }
    }

    // 查找对象映射的节点
    public String getObjectNode(String object) {
        long hash = FNVHash(object);
        SortedMap<Long, String> tailMap = virtualNodes.tailMap(hash); // 所有大于 hash 的节点
        Long key = tailMap.isEmpty() ? virtualNodes.firstKey() : tailMap.firstKey();
        return virtualNodes.get(key);
    }

    // 统计对象与节点的映射关系
    public void dumpObjectNodeMap(String label, int objectMin, int objectMax) {
        // 统计
        Map<String, Integer> objectNodeMap = new TreeMap<>(); // IP => COUNT
        for (int object = objectMin; object <= objectMax; ++object) {
            String nodeIp = getObjectNode(Integer.toString(object));
            Integer count = objectNodeMap.get(nodeIp);
            objectNodeMap.put(nodeIp, (count == null ? 0 : count + 1));
        }

        // 打印
        double totalCount = objectMax - objectMin + 1;
        System.out.println("======== " + label + " ========");
        for (Map.Entry<String, Integer> entry : objectNodeMap.entrySet()) {
            long percent = (int) (100 * entry.getValue() / totalCount);
            System.out.println("IP=" + entry.getKey() + ": RATE=" + percent + "%");
        }
    }

    public static void main(String[] args) {
        ConsistentHashing ch = new ConsistentHashing();

        // 初始情况
        ch.dumpObjectNodeMap("初始情况", 0, 65536);

        // 删除物理节点
        ch.removePhysicalNode("192.168.1.103");
        ch.dumpObjectNodeMap("删除物理节点", 0, 65536);

        // 添加物理节点
        ch.addPhysicalNode("192.168.1.108");
        ch.dumpObjectNodeMap("添加物理节点", 0, 65536);
    }
}

3.2 复制倍数为 1 时的均衡性

修改代码中 VIRTUAL_COPIES = 1(相当于没有虚拟节点)，运行结果如下(可见各节点负荷很不均衡)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
======== 初始情况 ========
IP=192.168.1.101: RATE=45%
IP=192.168.1.102: RATE=3%
IP=192.168.1.103: RATE=28%
IP=192.168.1.104: RATE=22%
======== 删除物理节点 ========
IP=192.168.1.101: RATE=45%
IP=192.168.1.102: RATE=3%
IP=192.168.1.104: RATE=51%
======== 添加物理节点 ========
IP=192.168.1.101: RATE=45%
IP=192.168.1.102: RATE=3%
IP=192.168.1.104: RATE=32%
IP=192.168.1.108: RATE=18%

3.2 复制倍数为 32 时的均衡性

修改代码中 VIRTUAL_COPIES = 32，运行结果如下(可见各节点负荷比较均衡)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
======== 初始情况 ========
IP=192.168.1.101: RATE=29%
IP=192.168.1.102: RATE=21%
IP=192.168.1.103: RATE=25%
IP=192.168.1.104: RATE=23%
======== 删除物理节点 ========
IP=192.168.1.101: RATE=39%
IP=192.168.1.102: RATE=37%
IP=192.168.1.104: RATE=23%
======== 添加物理节点 ========
IP=192.168.1.101: RATE=35%
IP=192.168.1.102: RATE=20%
IP=192.168.1.104: RATE=23%
IP=192.168.1.108: RATE=20%

3.2 复制倍数为 1M 时的均衡性

修改代码中 VIRTUAL_COPIES = 1048576，运行结果如下(可见各节点负荷非常均衡)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
======== 初始情况 ========
IP=192.168.1.101: RATE=24%
IP=192.168.1.102: RATE=24%
IP=192.168.1.103: RATE=25%
IP=192.168.1.104: RATE=25%
======== 删除物理节点 ========
IP=192.168.1.101: RATE=33%
IP=192.168.1.102: RATE=33%
IP=192.168.1.104: RATE=33%
======== 添加物理节点 ========
IP=192.168.1.101: RATE=25%
IP=192.168.1.102: RATE=24%
IP=192.168.1.104: RATE=24%
IP=192.168.1.108: RATE=24%

4 应用

一致性哈希是分布式系统组件负载均衡的首选算法，它既可以在客户端实现，也可以在中间件上实现。其应用有：

  • 分布式散列表(DHT)的设计；
  • 分布式关系数据库(MySQL)：分库分表时，计算数据与节点的映射关系；
  • 分布式缓存：Memcached 的客户端实现了一致性哈希，还可以使用中间件 twemproxy 管理 redis/memcache 集群；
  • RPC 框架 Dubbo：用来选择服务提供者；
  • 亚马逊的云存储系统 Dynamo；
  • 分布式 Web 缓存；
  • Bittorrent DHT；
  • LVS。
文章目录
  1. 1 概述
    1. 1.1 传统哈希(硬哈希)
    2. 1.2 一致性哈希(Consistent Hashing)
    3. 1.3 哈希指标
    4. 1.4 资料链接
  2. 2 算法原理
    1. 2.1 映射方案
      1. 2.1.1 公用哈希函数和哈希环
      2. 2.1.2 节点(Node)映射至哈希环
      3. 2.1.3 对象(Object)映射于哈希环
      4. 2.1.4 对象(Object)映射至节点(Node)
    2. 2.2 删除节点
    3. 2.3 增加节点
    4. 2.4 虚拟节点
  3. 3 算法实现
    1. 3.1 源码
    2. 3.2 复制倍数为 1 时的均衡性
    3. 3.2 复制倍数为 32 时的均衡性
    4. 3.2 复制倍数为 1M 时的均衡性
  4. 4 应用